文、意如
題目:
- 請撰寫一程式,讀取sklearn.datasets中的波士頓房價(Boston)資料集,此資料集有504筆資料,每筆資料有14個屬性如下:
| 欄位 | 說明 |
|---|---|
| CRIM | 按城鎮劃分的人均犯罪率 |
| ZN | 超過25,000平方英尺的土地劃為住宅用地的比例 |
| INDUS | 城鎮非零售商用土地的比例 |
| CHAS | Charles River虛擬變數(如果靠近河流,則為1;否則為0) |
| NOX | 一氧化氮濃度(以百萬分之幾為單位) |
| RM | 每個住宅的平均房間數 |
| AGE | 1940年之前建造自有單位的比例 |
| DIS | 到五個波士頓就業中心的加權距離 |
| RAD | 徑向公路的可達性指數 |
| TAX | 每10,000美元的全值財產稅率 |
| PTRATIO | 城鎮的師生比例 |
| B | 1000(Bk-0.63)^ 2,其中Bk是按城鎮劃分的黑人比例 |
| LSTAT | 低階人口狀況百分比 |
| MEDV | 自有住房的中位數價格(單位為1000美元) |
- 請建立一個線性迴歸機器學習模型,用此資料集中的'CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX', 'PTRATIO','B','LSTAT'來預測'MEDV'欄位。
- 請將資料集分為訓練集與測試集,其中測試集占20%,random_state=1。
- 列印此一模型的平均絕對誤差(mean absolute error, MAE)、均方誤差(mean squared error, MSE)、均方根誤差(root-mean-square error, RMSE),並依據輸入值進行房價預測。
(三)、 請依序回答下列問題:
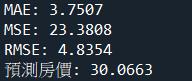
- 請填入測試資料集的平均絕對誤差MAE(四捨五入取至小數點後第四位)?
- 請填入測試資料集的均方誤差MSE(四捨五入取至小數點後第四位)?
- 請填入測試資料集的均方根誤差RMSE(四捨五入取至小數點後第四位)?
- 輸入資料為[0.00632, 18.00, 2.310, 0, 0.5380, 6.5750, 65.20, 4.0900, 1, 296.0, 15.30, 396.90, 4.98]。請填入預測房價(四捨五入取至小數點後第四位)?
MLD03.py
#from sklearn import datasets
#from sklearn.model_selection import cross_val_predict
#from sklearn import linear_model
# TODO
from sklearn.datasets import load_boston
boston = load_boston()
df = pd.DataFrame(boston.data.T, ['CRIM','ZN','INDUS','CHAS','NOX','RM' ,'AGE','DIS','RAD','TAX', 'PTRATIO','B','LSTAT']) #有13個feature
# TODO
# MEDV即預測目標向量
# TODO
X = df[['CRIM','ZN','INDUS','CHAS','NOX','RM' ,'AGE','DIS','RAD','TAX', 'PTRATIO','B','LSTAT']]
y = df['MEDV']
#分出20%的資料作為test set
# TODO
#Fit linear model 配適線性模型
# TODO
print('MAE:' )
print('MSE:' )
print('RMSE:' )
# ([[0.00632, 18.00, 2.310, 0, 0.5380, 6.5750, 65.20, 4.0900, 1, 296.0, 15.30, 396.90 , 4.98]])
prediction = lm.predict(X_new)
print( )
參考解答:
import pandas as pd
from sklearn.datasets import load_boston
boston = load_boston()
df = pd.DataFrame(boston.data.T, ['CRIM','ZN','INDUS','CHAS','NOX','RM' ,'AGE','DIS','RAD','TAX', 'PTRATIO','B','LSTAT']) #有13個feature
df = df.T
# MEDV即預測目標向量
df['MEDV'] = pd.Series(boston.target)
X = df[['CRIM','ZN','INDUS','CHAS','NOX','RM' ,'AGE','DIS','RAD','TAX', 'PTRATIO','B','LSTAT']]
y = df['MEDV']
#分出20%的資料作為test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
#Fit linear model 配適線性模型
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)
from sklearn.metrics import mean_absolute_error, mean_squared_error
test_MAE = mean_absolute_error(y_test, model.predict(X_test))
test_MSE = mean_squared_error(y_test, model.predict(X_test))
test_RMSE = (test_MSE)**0.5
print(f'MAE: {test_MAE:.4f}')
print(f'MSE: {test_MSE:.4f}')
print(f'RMSE: {test_RMSE:.4f}')
inp = [[0.00632, 18.00, 2.310, 0, 0.5380, 6.5750, 65.20, 4.0900, 1, 296.0, 15.30, 396.90 , 4.98]]
print(f"預測房價: {model.predict(inp)[0]:.4f}")程式解析:
# 匯入 pandas,用來進行資料處理
import pandas as pd
# 從 sklearn 載入波士頓房價資料集(注意:此資料集已在 sklearn 中標示為 deprecated)
from sklearn.datasets import load_boston
boston = load_boston() # 載入資料集
# 將原始資料轉置後轉成 DataFrame(13 個特徵),設定每列的欄位名稱
df = pd.DataFrame(boston.data.T, ['CRIM','ZN','INDUS','CHAS','NOX','RM' ,'AGE','DIS','RAD','TAX', 'PTRATIO','B','LSTAT'])
# 再次轉置,讓每一列代表一筆資料(行:樣本,列:特徵)
df = df.T
# 將房價(目標值 MEDV)加到 DataFrame 中作為最後一欄
df['MEDV'] = pd.Series(boston.target)
# X 是輸入特徵(13 欄),y 是目標值(房價)
X = df[['CRIM','ZN','INDUS','CHAS','NOX','RM' ,'AGE','DIS','RAD','TAX', 'PTRATIO','B','LSTAT']]
y = df['MEDV']
# 匯入 train_test_split 用來切分資料集
from sklearn.model_selection import train_test_split
# 將資料集分成訓練組與測試組,測試組佔 20%,設定隨機種子為 1
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
# 匯入線性回歸模型
from sklearn.linear_model import LinearRegression
# 建立線性回歸模型
model = LinearRegression()
# 使用訓練資料來訓練模型
model.fit(X_train, y_train)
# 匯入評估模型用的指標:MAE、MSE
from sklearn.metrics import mean_absolute_error, mean_squared_error
# 使用測試資料評估模型的表現(平均絕對誤差)
test_MAE = mean_absolute_error(y_test, model.predict(X_test))
# 平均平方誤差(越小越好)
test_MSE = mean_squared_error(y_test, model.predict(X_test))
# 均方根誤差(是 MSE 的平方根,單位與房價一致)
test_RMSE = (test_MSE)**0.5
# 輸出評估結果,保留 4 位小數
print(f'MAE: {test_MAE:.4f}')
print(f'MSE: {test_MSE:.4f}')
print(f'RMSE: {test_RMSE:.4f}')
# 測試一筆資料進行房價預測(共 13 個特徵)
inp = [[0.00632, 18.00, 2.310, 0, 0.5380, 6.5750, 65.20, 4.0900, 1, 296.0, 15.30, 396.90 , 4.98]]
# 使用訓練好的模型進行預測,並印出預測結果
print(f"預測房價: {model.predict(inp)[0]:.4f}")

Yiru@Studio - 關於我 - 意如
