[TQC+][Python][PML3]人工智慧：機器學習-305.台北房價預測

2025-07-20

文、意如

題目:

請撰寫程式讀取台北市房價資料集Taipei_house.csv，建立迴歸分析模型預測房價並分析其效能。資料集的欄位說明如下：

編號	欄位名稱	說明	編號	欄位名稱	說明
1	行政區*	包含4個區域	9	廳數
2	土地面積	平方公尺	10	衛數
3	建物總面積	平方公尺	11	電梯*	0：無 1：有
4	屋齡	年	12	車位類別*	共8種
5	樓層		13	交易日期	年月日
6	總樓層		14	經度
7	用途*	0：住宅用 1：商業用	15	緯度
8	房數		16	總價	萬元

＊備註：欄位有標示星號(*)者為類別變數，其餘為數值變數。 2. 進行「行政區」欄位的獨熱編碼（One-Hot encoding），並修改「車位類別」欄位：將欄位值="無"修改為0，其餘為1。 3. 將資料集分為訓練集與測試集，其中測試集占20%。 4. 建立四個迴歸模型（參數設定見待編修檔）：
a. 複迴歸。
b. 脊迴歸（Ridge regression）。
c. 多項式迴歸。
d. 多項式迴歸+Lasso迴歸。
5. 針對訓練集的15個欄位（編號2~12欄位+行政區的獨熱編碼4個欄位）進行上述四個迴歸模型的擬合，並分別對訓練集與測試集，計算效能評估指標均方根誤差Root Mean Squared Error（RMSE）以及調整R平方Adjusted R2。 6. 利用所有資料重新擬合模型，輸入一個屋況進行房價預測。

（三）、請依序回答下列問題：

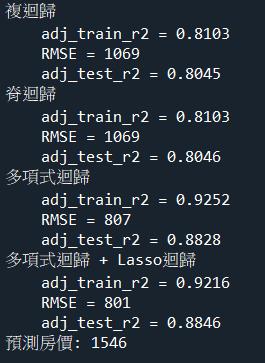
請填入四個迴歸模型對訓練集的最大Adjusted R2（四捨五入取至小數點後第四位）？
請填入四個迴歸模型對測試集的最小RMSE（計算至整數）？
請填入a. 複迴歸、b. 脊迴歸，兩個迴歸模型對測試集的最大Adjusted R2（四捨五入取至小數點後第四位）？
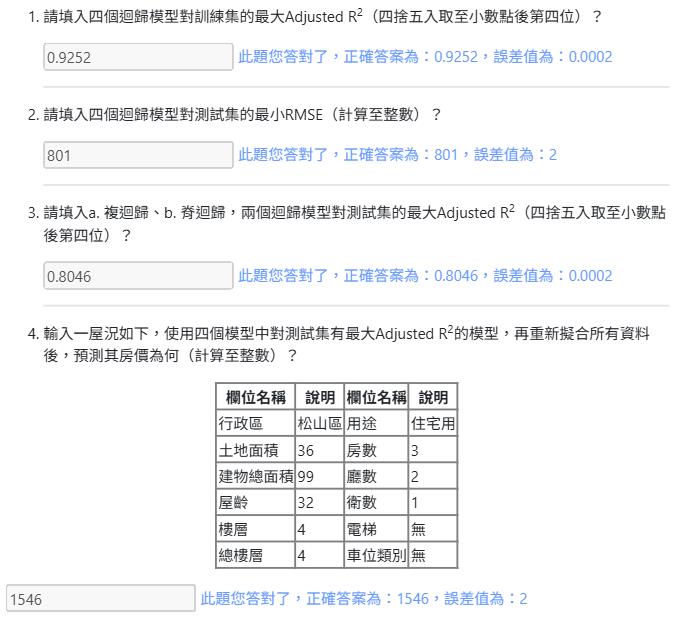
輸入一屋況如下，使用四個模型中對測試集有最大Adjusted R2的模型，再重新擬合所有資料後，預測其房價為何（計算至整數）？

欄位名稱	說明	欄位名稱	說明
行政區	松山區	用途	住宅用
土地面積	36	房數	3
建物總面積	99	廳數	2
屋齡	32	衛數	1
樓層	4	電梯	無
總樓層	4	車位類別	無

MLD03.py

# #############################################################################
# 本題參數設定，請勿更改
seed = 0   # 亂數種子數  
# #############################################################################
import warnings
warnings.filterwarnings('ignore')

import numpy as np
import pandas as pd 

# TODO

# 讀取台北市房價資料集
# TODO

# 對"行政區"進行 one-hot encoding
# TODO

# 處理"車位類別"
# TODO

# 計算 Adjusted R-squared
def adj_R2(r2, n, k):
    """ 函式描述：計算 Adjusted R-squared
    參數：
        r2:R-squared 數值
        n: 樣本數
        k: 特徵數

    回傳：
        Adjusted R-squared
    """
    return r2-(k-1)/(n-k)*(1-r2)

# TODO



# 切分訓練集(80%)、測試集(20%)
features= ['土地面積', '建物總面積', '屋齡', '樓層', '總樓層', '用途', 
           '房數', '廳數', '衛數', '電梯', '車位類別', 
           '行政區_信義區', '行政區_大安區', '行政區_文山區','行政區_松山區']
target = '總價'  
# TODO



# 複迴歸(參數皆為預設值)
# #########################################################################
# '行政區_信義區', '行政區_大安區', '行政區_文山區','行政區_松山區' 四個特徵是經過
# one-hot encoding 後產生，若欄位名稱不同可自行修改之。
# #########################################################################
from sklearn import linear_model
# TODO


# 脊迴歸(Ridge regression)，除以下參數設定外，其餘為預設值
# #########################################################################
# alpha=10
# #########################################################################
# TODO

# 多項式迴歸，除以下參數設定外，其餘為預設值
# #########################################################################
# degree=2
# #########################################################################
from sklearn.preprocessing import PolynomialFeatures
# TODO


# 多項式迴歸 + Lasso迴歸，除以下參數設定外，其餘為預設值
# #########################################################################
# alpha=10
# #########################################################################
# TODO


print('對訓練集的最大 Adjusted R-squared: %.4f' % max(evaluation['adj. R2 (train)']))
print('對測試集的最小 RMSE:%d' % min(evaluation['RMSE (test)']))
print('兩個模型對測試集的最大 Adjusted R-squared: %.4f' % 
      max(evaluation.loc[:1, 'adj. R2 (test)']))

''' 預測 '''
# 利用所有資料重新擬合模型，並進行預測
# TODO


#features= ['土地面積', '建物總面積', '屋齡', '樓層', '總樓層', '用途', 
#           '房數', '廳數', '衛數', '電梯', '車位類別', 
#           '行政區_信義區', '行政區_大安區', '行政區_文山區','行政區_松山區']

# TODO

參考答案:

# #############################################################################
# 本題參數設定，請勿更改
seed = 0   # 亂數種子數  
# #############################################################################
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd 
# 讀取台北市房價資料集
data = pd.read_csv('Taipei_house.csv')
df = data.copy()
# 對"行政區"進行 one-hot encoding
df = pd.get_dummies(df, columns=['行政區'])
# 處理"車位類別"
df["車位類別"] = [0 if x=='無' else 1 for x in df["車位類別"]]
# 計算 Adjusted R-squared
def adj_R2(r2, n, k):
    """ 函式描述：計算 Adjusted R-squared
    參數：
        r2:R-squared 數值
        n: 樣本數
        k: 特徵數
    回傳：
        Adjusted R-squared
    """
    return r2-(k-1)/(n-k)*(1-r2)
# 切分訓練集(80%)、測試集(20%)
features= ['土地面積', '建物總面積', '屋齡', '樓層', '總樓層', '用途', 
           '房數', '廳數', '衛數', '電梯', '車位類別', 
           '行政區_信義區', '行政區_大安區', '行政區_文山區','行政區_松山區']
target = '總價'  
X = df[features]
y = df[target]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=seed)
# 複迴歸(參數皆為預設值)
# #########################################################################
# '行政區_信義區', '行政區_大安區', '行政區_文山區','行政區_松山區' 四個特徵是經過
# one-hot encoding 後產生，若欄位名稱不同可自行修改之。
# #########################################################################
from sklearn import linear_model
multi = linear_model.LinearRegression()

# 脊迴歸(Ridge regression)，除以下參數設定外，其餘為預設值
# #########################################################################
# alpha=10
# #########################################################################
ridge = linear_model.Ridge(alpha=10)

# 多項式迴歸，除以下參數設定外，其餘為預設值
# #########################################################################
# degree=2
# #########################################################################
from sklearn.preprocessing import PolynomialFeatures
X_train_py = PolynomialFeatures(degree=2).fit_transform(X_train)
X_test_py = PolynomialFeatures(degree=2).fit_transform(X_test)
poly = linear_model.LinearRegression()

# 多項式迴歸 + Lasso迴歸，除以下參數設定外，其餘為預設值
# #########################################################################
# alpha=10
# #########################################################################
lasso = linear_model.Lasso(alpha=10)

name_list = ['複迴歸', '脊迴歸', '多項式迴歸', '多項式迴歸 + Lasso迴歸']
model_list = [multi, ridge, poly, lasso]
from sklearn.metrics import mean_squared_error
for name, model in zip(name_list, model_list):
    if name=='多項式迴歸':
        X_train, X_test = X_train_py, X_test_py
    model.fit(X_train, y_train)
    adj_train_r2 = adj_R2(model.score(X_train, y_train), X_train.shape[0], X_train.shape[1])
    RMSE = (mean_squared_error(y_test, model.predict(X_test)))**0.5
    adj_test_r2 = adj_R2(model.score(X_test, y_test), X_test.shape[0], X_test.shape[1])
    print(f"{name}\n\t"
          f"{adj_train_r2 = :.4f}\n\t"
          f"{RMSE = :.0f}\n\t"
          f"{adj_test_r2 = :.4f}")

''' 預測 '''
# 利用所有資料重新擬合模型，並進行預測
X_py = PolynomialFeatures(degree=2).fit_transform(X)
lasso.fit(X_py, y)
inp = pd.DataFrame([[36, 99, 32, 4, 4, 0, 3, 2, 1, 0, 0, 0, 0, 0, 1]])
inp = PolynomialFeatures(degree=2).fit_transform(inp)
print(f"預測房價: {lasso.predict(inp)[0]:.0f}")
#features= ['土地面積', '建物總面積', '屋齡', '樓層', '總樓層', '用途', 
#           '房數', '廳數', '衛數', '電梯', '車位類別', 
#           '行政區_信義區', '行政區_大安區', '行政區_文山區','行政區_松山區']

程式解析:

# #############################################################################
# 本題參數設定，請勿更改
seed = 0   # 設定亂數種子，使得訓練/測試切分可重現
# #############################################################################

# 忽略警告訊息，讓輸出畫面更乾淨
import warnings
warnings.filterwarnings('ignore')

# 匯入套件
import numpy as np
import pandas as pd 

# 讀取台北市房價資料集
data = pd.read_csv('Taipei_house.csv')
df = data.copy()  # 建立資料副本，避免直接修改原始資料

# 對"行政區"進行 one-hot 編碼，轉換為多個二元變數欄位
df = pd.get_dummies(df, columns=['行政區'])

# 將"車位類別"欄位轉換為數值，'無'=0，其餘=1
df["車位類別"] = [0 if x=='無' else 1 for x in df["車位類別"]]

# 定義計算 Adjusted R-squared 的函式
def adj_R2(r2, n, k):
    """ 計算調整後的 R-squared，考慮特徵數量的影響 """
    return r2 - (k - 1) / (n - k) * (1 - r2)

# 指定特徵欄位
features = ['土地面積', '建物總面積', '屋齡', '樓層', '總樓層', '用途', 
            '房數', '廳數', '衛數', '電梯', '車位類別', 
            '行政區_信義區', '行政區_大安區', '行政區_文山區', '行政區_松山區']
target = '總價'  # 預測目標：總價

# 特徵與標籤分開
X = df[features]
y = df[target]

# 切分訓練集與測試集 (80%/20%)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=seed)

# 匯入線性模型
from sklearn import linear_model

# 複迴歸模型 (Multiple Linear Regression)
multi = linear_model.LinearRegression()

# 脊迴歸 (Ridge Regression)，加入 alpha 抑制多重共線性
ridge = linear_model.Ridge(alpha=10)

# 多項式特徵轉換器 (degree=2，表示平方項)
from sklearn.preprocessing import PolynomialFeatures
X_train_py = PolynomialFeatures(degree=2).fit_transform(X_train)
X_test_py = PolynomialFeatures(degree=2).fit_transform(X_test)

# 多項式回歸模型（線性模型配合多項式特徵）
poly = linear_model.LinearRegression()

# 多項式 + Lasso 回歸模型，Lasso 有變數篩選效果
lasso = linear_model.Lasso(alpha=10)

# 設定模型名稱與模型清單
name_list = ['複迴歸', '脊迴歸', '多項式迴歸', '多項式迴歸 + Lasso迴歸']
model_list = [multi, ridge, poly, lasso]

# 匯入評估指標：RMSE
from sklearn.metrics import mean_squared_error

# 逐一訓練各種模型並輸出訓練結果
for name, model in zip(name_list, model_list):
    if name == '多項式迴歸':
        # 使用多項式特徵資料
        X_train, X_test = X_train_py, X_test_py
    model.fit(X_train, y_train)  # 訓練模型
    # 計算訓練集的 adjusted R-squared
    adj_train_r2 = adj_R2(model.score(X_train, y_train), X_train.shape[0], X_train.shape[1])
    # 計算測試集的 RMSE
    RMSE = (mean_squared_error(y_test, model.predict(X_test)))**0.5
    # 計算測試集的 adjusted R-squared
    adj_test_r2 = adj_R2(model.score(X_test, y_test), X_test.shape[0], X_test.shape[1])
    # 印出評估結果
    print(f"{name}\n\t"
          f"{adj_train_r2 = :.4f}\n\t"
          f"{RMSE = :.0f}\n\t"
          f"{adj_test_r2 = :.4f}")

''' 預測 '''

# 使用所有資料重新訓練多項式+Lasso模型
X_py = PolynomialFeatures(degree=2).fit_transform(X)
lasso.fit(X_py, y)

# 建立新樣本進行預測，欄位順序需與特徵相同
inp = pd.DataFrame([[36, 99, 32, 4, 4, 0, 3, 2, 1, 0, 0, 0, 0, 0, 1]])
inp = PolynomialFeatures(degree=2).fit_transform(inp)

# 預測新資料的總價
print(f"預測房價: {lasso.predict(inp)[0]:.0f}")

Yiru@Studio - 關於我 - 意如

TQC+Python-人工智慧-機器學習

回首頁

Yiru@Studio

Yiru@Studio

[TQC+][Python][PML3]人工智慧：機器學習-305.台北房價預測

題目:

MLD03.py

程式解析:

標籤雲

系列文章